Electronics Components Distributor

기본 논리 게이트 및 부울 표현
2024-05-10 9850

디지털 전자 장치의 영역에서 논리 게이트와 부울 표현의 기본 개념을 이해하는 것이 신진 엔지니어와 노련한 엔지니어 모두에게 가장 중요합니다.이 기사는 디지털 회로의 핵심 구성 요소 인 논리 게이트의 기본 사항을 탐구하여 현대 컴퓨팅을 뒷받침하는 이진 의사 결정 프로세스의 기초를 마련합니다.논리 게이트는 디지털 회로의 논리를 단순화하고 분석하는 데 사용되는 중요한 프레임 워크 인 부울 대수의 규칙에 따라 이진 신호를 조작합니다.주로 트랜지스터로 구성된이 게이트는 전기 입력을 이진 출력으로 변환합니다. 이진 값은 각각 1과 0의 이진 값에 해당합니다.이 문서는 Not, OR, OR, XOR, NAND 및 NOR과 같은 다양한 유형의 논리 게이트의 운영 원리, 상징적 표현 및 실질적인 응용 프로그램을 탐구합니다.

1. 로직 게이트 개요

그림 1 : 기본 로직 게이트 회로 그래픽 기호

로직 게이트 개요

논리 게이트는 주로 트랜지스터로 구성된 통합 회로의 기본 빌딩 블록입니다.각 게이트는 전기 신호를 조작하기 위해 특정 방식으로 트랜지스터를 결합합니다.신호가 이러한 게이트를 통과함에 따라, 높은 수준 또는 낮은 레벨로 나타나서 필수적으로 전기 입력을 이진 출력으로 전환합니다.이 높고 낮은 상태는 1과 0의 이진 값 또는 논리적 "true"및 "false"에 해당합니다.이 변환은 논리적 작업을 수행하기위한 기초입니다.

가장 일반적인 유형의 논리 게이트는 그렇지 않은 것, 또는 xor, nand 및 gates입니다.각 게이트는 고유하게 기능합니다.

Not Gate는 단일 입력을 가져 와서 뒤집습니다.입력이 높으면 출력이 낮고 그 반대도 마찬가지입니다.

AN 및 게이트는 모든 입력이 높은 경우에만 높은 신호를 출력합니다.

OR 게이트는 하나 이상의 입력이 높으면 높은 출력을 제공합니다.

XOR 게이트는 홀수의 입력이 높은 경우에만 높은 출력을 제공합니다.

NAND 게이트는 AN 및 게이트와 유사하지만 모든 입력이 높으면 낮은 신호를 출력합니다.

NOR 게이트는 OR 게이트처럼 작동하지만 입력이 높으면 출력이 낮습니다.

이러한 게이트를 다양한 구성으로 결합함으로써보다 복잡한 논리 기능을 실행하여 컴퓨터 및 기타 디지털 장치에서 정교한 작업 및 의사 결정 프로세스를 용이하게합니다.각 논리 게이트는 디지털 시스템이 정보를 처리하고 계산하는 방식에 큰 역할을합니다.

게이트가 아닙니다

일반적으로 인버터로 알려진 Not Gate는 디지털 회로의 기본 구성 요소입니다.설계에는 입력 및 출력 끝이 포함되며, 출력은 일반적으로 신호 역전을 나타내는 원으로 표시됩니다.이 간단한 구성을 사용하면 게이트가 아닌 입력을 반전시킬 수 있습니다. 높은 신호 (논리적 "true")가 낮아지고 (논리적 "거짓") 그 반대도 마찬가지입니다.

그림 2 : 논리 게이트의 3 가지 기호

기호 측면에서, NOT 게이트는 다양한 표준에 따라 다르게 표현됩니다.ANSI/IEEE STD 91-1984는 모양 특성 기호를 사용하는 반면 IEC 60617-12는 직사각형 국가 표준 기호를 사용합니다.더 이상 사용하지는 않지만 DIN 40700은 역사적으로 다른 심볼 세트를 제공했습니다.

응용 프로그램에 중점을 둔 NOT GATE는 디지털 회로의 중요한 빌딩 블록 역할을합니다.하나의 일반적인 사용법은 래치를 만드는 것입니다.이는 두 순차 인버터의 출력을 1 비트 레지스터의 입력에 다시 연결하여 기본 메모리 요소를 형성하여 수행됩니다.Not Gates의 실제 적용의 예는 6 개의 개별 인버터를 포함하는 통합 회로 인 Hexa-inverter입니다.예를 들어, 7404 TTL 칩과 4049 CMOS 칩은 모두 6 개의 인버터를 통합합니다.이 칩에는 전원 공급 장치/기준 전압 용 2 개의 핀과 인버터 전용 핀을 포함하여 각각 14 및 16 핀으로 설계되었지만 4049 칩에는 연결되지 않은 2 개의 핀이 있습니다.

그리고 게이트

디지털 회로의 기본 구성 요소 인 and Gate는 종종 "및 회로"및 "논리"제품 "및 논리적"및 "회로"를 포함한 여러 이름으로 언급됩니다."및"작업을 수행하여 작동하므로 여러 입력이 필요하고 하나의 출력이 생성됩니다.모든 입력이 동시에 높을 때 AN 및 게이트의 출력은 높아집니다 (논리 1).입력이 낮 으면 (논리 0) 출력도 낮습니다.이 작업은 수학적으로 y = a × b로 표현 될 수 있습니다.

기호 측면에서, 및 게이트는 다른 표준에 따라 여러 가지 방법으로 표시됩니다. Ansi/IEEE STD 91-1984에 따른 모양 특성 기호, IEC 직사각형 국가 표준 기호 (IEC 60617-12) 및 오래된 DIN 기호(DIN 40700).

게이트는 CMOS, NMOS, PMOS 및 다이오드 기반 로직을 포함한 다양한 기술을 사용하여 구현할 수 있습니다.이 다목적 성은 TTL (트랜지스터-트랜지스터 로직) 및 CMO (보완 금속 산화물-비도체) 통합 회로에 포함되어 현대 전자 제품에 필수적입니다.

통합 회로의 구현 및 게이트가 널리 퍼져 있습니다.예를 들어, 표준 74 시리즈 CMOS 회로에는 다음이 포함됩니다.

74x08 및 74x09 (OC), 각각 4 개의 독립적 인 2 입력 및 게이트를 포함하고;

3 개의 독립적 인 3 입력 및 게이트를 포함하는 74x11;

74x21은 두 개의 독립적 인 4 입력 및 게이트를 특징으로합니다.

마찬가지로, 또 다른 일반 가족 인 CD4000 시리즈 통합 회로에는 다음이 포함됩니다.

4 개의 2 입력 및 게이트가있는 CD4081,

두 개의 4 입력 및 게이트를 포함하는 CD4082.

이러한 통합 회로는 일반적으로 여러 조건에 따라 정확한 논리 제어 및 의사 결정이 필요한 다양한 디지털 장치에서 사용됩니다.각 유형의 회로는 특정 입력 구성을 제공하여 디지털 시스템에서 유연하고 맞춤형 애플리케이션을 제공합니다.

그림 3 : 74x21

그림 4 : CD4081

또는 게이트

"또는 회로"라고도하는 OR 게이트는 여러 조건을 평가하는 디지털 로직에서 중요한 요소입니다.적어도 하나의 조건이 충족되면, 즉 또는 게이트에 대한 입력 중 하나 이상이 높으면 (논리 1) 출력이 높게 설정됩니다 (논리 1).반대로, 출력은 모든 입력이 낮을 때만 낮습니다 (논리 0).이 바이너리 논리는 "또는"논리적 관계의 기초를 형성하며, 이는 사건의 발생이 여러 조건 중 하나의 만족도에 달려 있음을 규정합니다.

실제적인 용어로, 또는 게이트는 디지털 회로에서 광범위하게 사용되어 여러 입력 중 하나 이상이 사실이어야하는 결정을 처리합니다.예를 들어, OR 게이트는 여러 센서 중 하나가 트리거되면 활성화되는 메커니즘을 제어 할 수 있습니다.이 게이트를 결합하여보다 복잡한 입력 배열을 관리 할 수 있습니다.예를 들어, 여러 2 입력 또는 게이트를 연결하여 처리 조건의 수를 확장하여보다 복잡한 회로 설계에서 유틸리티를 향상시킬 수 있습니다.

XOR 게이트로 이동하는이 구성 요소는 논리적 XOR 작업을 구현하여 디지털 로직의 특정 기능을 사용합니다.XOR 게이트에는 2 개의 입력 단자와 1 개의 출력 단자가 있습니다.입력 레벨이 다를 때 높은 출력 (논리 1)과 입력이 동일 할 때 낮은 출력 (논리 0)을 제공합니다.이 고유 한 기능을 사용하면 XOR 게이트가 이진 첨가를 계산하는 데 기본적인 모듈로 2를 수행 할 수 있습니다.

XOR 게이트의 동일한 입력 상태와 다른 입력 상태를 구별 할 수있는 용량은 특히 절반과 같은 산술 회로에서 유용합니다.두 개의 단일 바이너리 숫자를 추가하는 하프 어드더는 XOR 게이트와 및 게이트를 사용하여 구성됩니다.XOR 게이트는 합산 작업을 처리하는 반면 및 게이트는 다음 더 높은 비트에 이월이 있는지 여부를 결정합니다.XOR 작동에 대한 논리적 표현은 다음과 같이 표시됩니다. .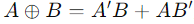

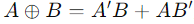그림 5 : XOR 게이트

NAND 게이트

NAND GATE는 본질적으로 AN과 게이트와 NAT 게이트의 조합으로, 두 작업을 순차적으로 수행하도록 설계되었습니다.AN 및 작동으로 시작하여 두 개의 입력을 취한 다음 결과에 작동하지 않는 작업을 적용합니다.NAND 게이트의 역학은 간단합니다. 두 입력이 모두 높으면 (논리 1에서) 출력이 낮습니다 (논리 0).그러나 입력이 낮 으면 (논리 0) 출력이 높습니다 (논리 1).이러한 및 게이트 출력의 역전은 NAND 게이트를 디지털 회로의 중요한 구성 요소로 만듭니다.NAND 게이트의 논리적 표현은 다음과 같습니다 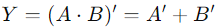, 그리고 작동 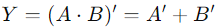후 반전을 강조합니다.

그림 6 : NAND 게이트 진실 테이블

DTL (Diode-Transissistor Logic) NAND 게이트 회로와 같은 실제 시나리오에서 다이오드와 게이트와 트랜지스터가 아닌 트랜지스터의 조합이 일반적입니다.이러한 구성은 게이트가 직렬로 연결될 때 발생하는 레벨 편차를 처리하고 부하 용량을 향상시키는 것을 목표로합니다.이 회로의 구성 요소 (디오드, 트랜지스터, 저항기 및 연결선)는 일반적으로 반도체 칩에 통합되어 통합 회로라고 알려진 것을 형성합니다.

DTL 회로는 간단한 구조에도 불구하고 작동 속도가 느리기 때문에 호의적으로 떨어졌습니다.한편, DTL의 수정 인 TTL (트랜지스터-트랜지스터 로직) 회로는 계속 널리 사용되고있다.이러한 개선에는 입력 스테이지의 설계가 포함되며, 멀티 이미 터 트랜지스터가 간단한 다이오드와 게이트를 대체하여 스위칭 속도를 향상시킵니다.이 배열은보다 효과적인 증폭을 허용하여 트랜지스터가 포화 될 때 과량 저장 전하를 빠르게 제거 할 수 있도록 더 강한 역 기본 전류를 제공하여 턴 오프 속도를 크게 향상시킵니다.출력 트랜지스터의 턴온 속도를 높이려면 다이오드 회로는 논리를 유지하는 트랜지스터로 교체 할 수 있습니다. 회로 동안 증폭을 향상시키는 동안 관계 활성화.이것은 출력에 더 큰 기본 전류를 제공하는 데 도움이됩니다. 트랜지스터, 활성화 속도.마지막으로, 출력 단계는 강력한 부하 용량을 갖도록 설계되었습니다. 이것은 기존 수집기 부하 저항을 대체하여 달성됩니다. 추가 트랜지스터 및 저항으로 구성된 활성 부하. 두 개의 보완 신호로 구동되는이 푸시 풀 구성, 한 트랜지스터가 항상 켜져 있고 다른 하나는 꺼져 있는지 확인하고 꾸준하고 효율적인 작동을 유지합니다.

그림 7 : DTL NAND 게이트 회로

게이트도

NOR 게이트는 논리적 또는 기능을 수행하도록 설계되었습니다.일반적으로 여러 개의 입력이 있지만 하나의 출력 만 있습니다.NOR GATE는 모든 입력이 낮은 경우에만 높은 출력 (논리 1)을 제공하도록 작동합니다 (논리 0).입력이 높으면 (논리 1) 출력은 즉시 낮음으로 전환됩니다 (로직 0).이 동작은 NOR 작동을 캡슐화하여 다양한 조합과 구성을 통해서가 아니라 다른 기본 논리 함수를 구현하는 데 사용할 수있는 범용 게이트가됩니다.

그림 8 : 게이트 IEC 60617-12

그림 9 : CMOS 로직

NOR 게이트의 다양성은 그 자체로 복잡한 논리적 기능을 만들 수있는 능력에 반영됩니다.이 독특한 특성은 ANSI/IEEE STD 91-1984 및 IEC 60617-12 표준으로 상징하며,이 표준은 이러한 게이트에 대한 뚜렷한 그래픽 표현을 제공합니다.ANSI/IEEE 표준은 Shape-Characteristic 기호를 사용하는 반면 IEC 표준은 직사각형 기호를 사용합니다.게이트는 TTL (트랜지스터-트랜지스터 로직) 및 CMO (보완 금속-산화물 반도체) 회로에서 발견되는 기본 구성 요소입니다.그들은 특히 표준 논리 칩에서 널리 퍼져 있습니다.

그림 10 : NAND 게이트를 통한

그림 11 : CD4001

CMOS 4000 시리즈에서 CD4000은 단일 NOT 게이트와 함께 2 개의 3 입력 및 게이트를 특징으로하며 CD4001에는 4 개의 2 입력 및 게이트가 포함되며 CD4002에는 2 개의 4 입력 및 게이트가 있습니다.

그림 12 : CD4000

그림 13 : CD4002

TTL 74 시리즈에서 74x02는 4 개의 2 입력 및 게이트를 제공하며 74x27에는 3 개의 3 입력 및 게이트가 포함되어 있으며 7428은 2 개의 4 입력 및 게이트를 제공합니다.

그림 14 : 74x02

그림 15 : 74x27

부울 표현

프로그래밍에서 부울 표현식은 두 가지 가능한 값 중 하나 인 True 또는 False로 평가됩니다.가장 간단하게, 부울 표현식은 '2 == 4'표현과 같이 하나의 값이 다른 값과 같은지 확인합니다.이 표현은 2가 같지 않기 때문에 거짓으로 평가됩니다.,는 평가를 위해 런타임 상태에 의존하며 객체 속성의 현재 값을 기반으로 true 또는 false를 산출 할 수 있습니다.

C, C ++ 및 C#과 같은 프로그래밍 언어에서는 부울 표현식으로 사용되는 평등 연산자 인 '=='를 구별하는 것이 중요합니다.이러한 연산자를 잘못 사용하면 프로그램을 컴파일 할 때 또는 실행 중에 오류가 발생할 수 있습니다.부울 표현은 부울 피연산자와 논리 연산자를 사용하여 구성되어 특정 구문 규칙을 준수합니다.운영자는 다음과 같습니다.

논리적이고 (∧)

논리적 또는 (∨)

논리적이지 않음 (¬)

일부 프로그래밍 컨텍스트에서는 동등성과 같은 추가 연산자가≡) 및 의미 (→)도 사용됩니다.이러한 표현에는 부울 변수, 관계형 표현 (비교 이상의 비교) 및 괄호 안에 캡슐화 된 기타 부울 표현이 포함될 수 있습니다.관계 적 표현의 참 또는 거짓 가치 (예 : E1 < E2) is determined by the comparison of E1 and E2, which are arithmetic expressions. If E1 is indeed less than E2, the expression evaluates to true, otherwise false. In programming, Boolean expressions serve two primary functions:they are used as conditions to control the flow in various control structures and they can compute logical values directly. The precedence of operations in Boolean expressions typically follows this order:

괄호

산술 연산자 (*, /, +, -, %)

관계형 운영자 (<, <=, =, >,> =, <>)

논리 연산자 (¬, ∧, ∨)

평가 효율을 위해, 때로는 부울 표현을 평가할 필요가 없습니다.예를 들어, 'a ∨ b'표현에서 A가 사실이라면 B에 관계없이 전체 표현이 사실입니다.이 개념은 결과가 이미 결정되면 평가가 일찍 중지 될 수있는 "단락"이라는 아이디어를 소개합니다.표현의 일부로.'a∨ (b∧ (¬c∨d))와 같은 복잡한 부울 표현식에서 구조화 된 평가를 사용하면 컴파일러 설계에 종종 사용되는보다 효율적인 중간 코드 생성으로 이어질 수 있습니다.'a', 'b', 'c'및 'd'의 값에 따라 평가 경로와 결과는 다를 수 있으며, 그 결과를 결정적으로 결정하는 표현의 점을 강조 표시합니다.이 종료는 계산 프로세스에서 제어 흐름 방향을 나타냅니다. 부울 값이 참 또는 거짓으로 평가되는 것처럼 제어가 진행되어야하는지 여부를 안내합니다.이 메커니즘은 프로그래밍에서 제어 구조를 설계하는 데 중추적이며 부울 논리를 기반으로 동적 및 조건부 실행 경로를 허용합니다.

부울 표현의 진실 값을 결정하는 E는 문법 번역 중에 전개되는 체계적인 과정입니다.'e = e (1) ∨ e (2)와 같은 표현을 고려해 봅시다.e (1)이 true로 평가되면 전체 표현식 'e'는 true이며, 'e (1)'의 실제 종말점은 또한 'e'의 진정한 종말점입니다.그러나 'e (1)'이 거짓이면 e의 값은 'e (2)'에 따라 다릅니다.이 시나리오에서 'E (2)'는 다음에 평가되어야합니다.'e (1)'의 잘못된 종말점은 우리를 'E (2)'의 시작으로 안내하고 'E (2)'의 참와 거짓 결과는 'e'에 대한 해당 결과를 정의합니다.

부울 식 번역 알고리즘을 생성 할 때 여러 유형의 제어 쿼터니언이 사용됩니다.

(JNZ, A1 ,, P) -'A1'이 참 (0이 아닌) 인 경우 Quaternion p로 이동합니다.

(Jrop, A1, A2, P) - 'A1 ROP A2'관계가 사실이라면 Quaternion P로 이동합니다.

(J ,, P) - 무조건 Quaternion으로 점프 p.

예를 들어, 조건부 진술에서 'A ∨ b. < C then S1 else S2', the translated quaternion sequence might look like this:

(jnz, a, -, 5) - A가 참이면 S1의 동작으로 직접 이동하십시오.

(J, -, -, 3) - 'B'를 평가하기위한 무조건적인 점프 < 'C'.

(제이 <, B, C, 5) - 경우 b < C is true, jump to execute S1.

(J, -, -, P+1) - S1에 대한 Quaternion 시퀀스가 뒤 따릅니다.

(p) (j, -, -, q) - S1 이후 S2의 실행 또는 A 또는 B가 아닌 경우 < C is true.

상향식 문법 유도 번역에서, 제어 쿼터니온이 생성 될 때, 대상 쿼터니온은 아직 존재하지 않을 수 있으며, 초기에 불완전한 제어 전송이 발생할 수 있습니다.예를 들어, '(jnz, a, -, 0)'은 A (또는 S1의 시작점)의 실제 종말점이 아직 알려지지 않았기 때문에 자리 표시 자로 생성 될 수 있습니다.이 자리 표시자는 목적지가 명확 해지면 업데이트됩니다.번역하는 동안 여러 쿼터니언이 결정되지 않은 대상을 가리키는 것이 일반적입니다.이들은 대상이 정의되면 함께 연결되어 업데이트됩니다.이 구문 유도 변환에서는 문법을 재구성하여 True 및 False exit 체인 (TC 및 FC)과 같은 시맨틱 속성이 적시에 캡처되도록하는 것이 도움이됩니다.

expr ∧ ® expr ∧

expr ∨ ® expr ∨

문법 의이 "분할"을 통해 연산자의 왼쪽에 TC 및 FC의 표현에 즉시 액세스 할 수 있습니다.이러한 속성이 알려지면 다음 사용 가능한 쿼터니언 번호를 사용하여 이전 표현식의 각 TC 또는 FC를 채우는 데 사용할 수 있습니다.이 구조화 된 접근법은 논리적 정밀도가 전기 회로 제어와 매우 유사한 논리적 정밀도가 프로그램 흐름 및 작동을 지시하는 프로그래밍에서 복잡한 제어 구조를 효과적으로 관리하는 데 필수적입니다.

결론

논리 게이트와 부울 표현의 복잡한 춤은 디지털 로직 디자인의 중추를 형성하여 정교한 전자 장치 및 시스템의 구성을 가능하게합니다.이 기사는 각 게이트 기능과 더 큰 회로 내에서의 역할에 대한 자세한 탐구를 통해 간단한 이진 결정이 복잡한 계산 작업으로 어떻게 확대되는지를 밝힙니다.기본 메모리 요소에서 고급 통합 회로에 이르기까지 실제 응용 분야의 탐색은 현대 기술에서 이러한 구성 요소의 다양성과 필수 특성을 강조합니다.이론적 지식을 실용적인 응용 프로그램과 통합함으로써 논리 게이트 및 부울 표현에 대한 연구는 학문적이고 전문적인 추구를 풍부하게 할뿐만 아니라 디지털 전자 제품 분야를 추진합니다.

자주 묻는 질문 [FAQ]

1. 논리 게이트와 부울 표현의 차이점은 무엇입니까?

로직 게이트는 특정 규칙에 따라 단일 출력을 생성하기 위해 하나 이상의 이진 입력에서 논리적 작동을 수행하는 물리적 장치 (또는 회로 설계의 모델)입니다.일반적으로 디지털 회로의 트랜지스터에 의해 하드웨어로 표시됩니다.

반면에 부울 표현은 참 또는 거짓의 두 값 중 하나로 평가하는 수학적 표현입니다.부울 표현은 논리 연산자를 사용하며 논리 작업을 대수적으로 설명하기 위해 프로그래밍 및 이론적 컴퓨터 과학에 사용됩니다.

2. 7 논리 게이트는 무엇입니까?

및 게이트 : 모든 입력이 참인 경우에만 출력은 사실입니다.

또는 게이트 : 적어도 하나의 입력이 true 인 경우 출력이 true입니다.

게이트가 아님 (인버터) : 입력의 반대를 출력합니다.

NAND GATE : 모든 입력이 참인 경우에만 False를 출력합니다.

게이트 : 모든 입력이 거짓 인 경우에만 출력이 참전됩니다.

XOR 게이트 (독점 또는) : 입력이 다른 경우 출력이 적용됩니다.

xnor gate (독점 NOR) : 입력이 동일하면 출력이 적용됩니다.

3. 부울 표현의 예는 무엇입니까?

부울 표현의 예는 'a and not b'입니다.이 표현은 A가 참이고 B가 False 인 경우에만 TRUE로 평가합니다.논리적 인 용어로는 'a∧ob'로 쓸 수 있습니다.

4. 세 가지 유형의 논리 게이트는 무엇입니까?

"Type"에 의해 기능을 기반으로 클래스를 의미하는 경우, 논리 게이트의 세 가지 기본 범주는 다음과 같습니다.

기본 게이트 : 그리고 또는 또는 그렇지 않습니다

유니버설 게이트 : NAND, 또는 (다른 유형의 게이트를 구성하는 데 사용될 수 있음)

전문 게이트 : Xor, Xnor (패리티 검사 및 평등과 같은 특정 기능에 사용)

5. 논리 게이트를 식별하는 방법은 무엇입니까?

논리 게이트는 그들의 상징과 진실 표로 식별 할 수 있습니다.

각 게이트는 예를 들어 뚜렷한 기호를 가지며 게이트는 평평한 쪽을 가로 지르는 선이있는 D 자형으로 그려 지거나 게이트는 출력 지점으로 구부러집니다.입력 가능성과 해당 출력을 나열하는 테이블을 검사하십시오.예를 들어, Gate의 진실 테이블은 모든 입력이 높은 경우 (1) 만 나타납니다 (1).

출력 트랜지스터의 턴온 속도를 높이려면 다이오드 회로는 논리를 유지하는 트랜지스터로 교체 할 수 있습니다. 회로 동안 증폭을 향상시키는 동안 관계 활성화.이것은 출력에 더 큰 기본 전류를 제공하는 데 도움이됩니다. 트랜지스터, 활성화 속도.

우리에 대해 매번 고객 만족.상호 신뢰와 공통 관심사. ARIAT 기술
기능 검사.비용 효율적인 제품과 최고의 서비스는 우리의 영원한 헌신입니다.